Question

The equation d=65t models the distance, d, that Malcolm's family travels after t hours. 10 miles per hour 15 miles per hour 30 miles per hour 65 miles per hour

Answer 1

The question is incomplete. Here is the complete question.

Malcolm and Theo's families are both traveling to the same vacation resort. The equation d = 65t models the distance, d, that Malcolm's family travels after t hours.

The graph below shows the relationship between the distance and the amount of time that Theo's family traveled.

How much faster did Malcolm's family travel than Theo's family?

a) 10 miles per hour

b) 15 miles per hour

c) 30 miles per hour

d) 65 miles per hour

Answer: b) 15 miles per hour

Explanation: Speed is given by the change in distance per change in time or:

`v=(\Delta x)/(\Delta t)`

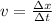
For Theo's family, the graph shows the change in miles is constant in hours, so, the speed they are traveling is

`v_(T)=(200-0)/(4-0)`

`v_(T)=(200)/(4)`

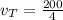
`v_(T)=` 50 mph

For Malcolm's family:

At t = 0: d = 65*0 = 0

At t = 4: d = 65*4

Then, Speed is:

`v_(M)=(65*4-0)/(4-0)`

`v_(M)=(65.4)/(4)`

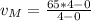
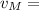`v_(M)=` 65 mph

Theo travels at 50 mph and Malcolm at 65 mph, therefore, Malcolm is 15 miles per hour faster than Theo