Question

Triangles ABC and d e f are similar the lengths of the sides of ABC are 56/64 and 72 the length of the largest side of d e f is 252 what is the length of the smallest side of d e f

Answer 1

`D E F = 196`

Explanation:

Given

`ABC = 56, 64\ and\ 72`

`Largest\ of\ D E F = 252`

Required

Determine the smallest side of DEF

Since both sides are similar, then the sides of DEF can be calculated using:

`D E F = k * ABC`

First, we need to solve for k

From the given parameters

`D E F = 252` when
`ABC = 72`

This is so because these are the largest sides of both triangles respectively

`D E F = k * ABC`

`252 = k * 72`

Divide through by 72

`252/72 = k * 72/72`

`k=252/72`

`k=3.5`

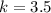
We make use of the same formula to determine the length of the smallest side.

The smallest of ABC is 56, so we have:

`D E F = k * ABC`

`D E F = 3.5 * 56`

`D E F = 196`

Hence, the smallest side of DEF is 196