Question

The residual for a predicted relative abundance when the rainfall was 3 inches is 1.25. What is the actual relative abundance when the rainfall was 3 inches

Answer 1

The actual relative abundance will be "7.59".

Explanation:

• The residual on something like a curve anywhere at a point becomes expressed as the maximum at either the position between some of the real y-value as well as the expected y-value.
• Consequently, the difference regarding true relative abundance as well as expected relative abundance seems to be 1.25 whether we presume that the x-variable represents rainfall, as well as they-variable, represents the relative abundance of locusts.

The predicted relative abundance for 3 inches rainfall will be:

=
`6.7 - (0.12* 3)`

=
`6.34`

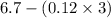
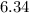
The residual will be:

=
`actual - predicted \ relative \ abundance`

=
`1.25`

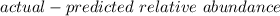
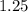
Now,

The actual relative abundance will be:

=
`1.25 + predicted \ relative \ abundance`

=
`1.25 + 6.34`

=
`7.59`

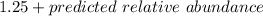
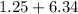
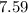
Remember that perhaps the residual positive value means that even the calculation underestimates the relative abundance. The real relative abundance, however, is 7.59.