Question

You purchased concentrated cleaner that must be diluted before use. Container a is the cleaner, which is 20% solution. Container b is pure water. You are mixing together the contents of container a and container b to produce 40 gallons of 9% solution. How many gallons from each container are needed to create the 40 gallons of 9% cleaning solution?

Answer 1

18 gallons from container
`a` and 22 gallons from the container
`b` to be mixed to get the required mixture.

Explanation:

Given that the container
`a` has 20% concentrated cleaner

and container
`b` has pure water which has 0% cleaner.

Let x gallons from container a and y gallons from the container b are mixed to get a 9% concentrated solution.

So,

`9\%\; \text{of}\; (x+y) = (20\% \; \text{of}\; x )+(0\% \; \text{of}\; y)\cdots(i)`

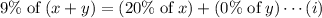
As the total amount of the final solution= 40 gallons

So,
`x+y=40\cdots(ii)`

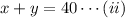
Using the value of equation (ii) in equation (i), we have

9% of 40 = 20% of x

`\Rightarrow 0.09* 40=0.2 * x`

`\Rightarrow x=(0.09* 40)/(0.2)`

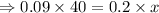
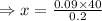
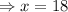`\Rightarrow x=18` gallons.

From equation (ii),

18+y=40

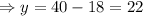`\Rightarrow y=40-18=22` gallons.

Hence, 18 gallons from container
`a` and 22 gallons from the container
`b` to be mixed to get the required mixture.