Question

"A waiter believes the distribution of his tips has a model that is slightly skewed to the left​, with a mean of ​$10.60 and a standard deviation of ​$6.60. He usually waits on about 50 parties over a weekend of work. ​a) Estimate the probability that he will earn at least ​$600. ​b) How much does he earn on the best 1​% of such​ weekends?"

Answer 1

(a) 0.0668

(b) $638.74

Explanation:

Let X denote the tips earned by a waiter.

It is provided that X follows a left-skewed distribution with mean, μ = $10.60 and standard deviation, σ = $6.60.

It is also provided that, the waiter usually waits on about n = 50 parties over a weekend of work.

According to the Central Limit Theorem if we have a population with mean μ and standard deviation σ and we take appropriately huge random samples (n ≥ 30) from the population with replacement, then the distribution of the sum of values of X, i.e ∑X, will be approximately normally distributed.

Then, the mean of the distribution of the sum of values of X is given by,

`\mu_(S)=n\mu\\`

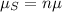
And the standard deviation of the distribution of the sum of values of X is given by,

`\sigma_(S)=√(n)\sigma`

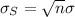
As the sample size is large, i.e. n = 50 > 30, the Central Limit Theorem can be used to approximate the sampling distribution of total tips by the normal distribution.

The mean and standard deviation are:

`\mu_(S)=50* 10.60=530\\\\\sigma_(S)=√(50)* 6.60=46.67`

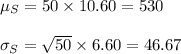
(a)

Compute the probability that he will earn at least $600 as follows:

`P(S\geq 600)=P((S-\mu_(S))/(\sigma_(S))\geq (600-530)/(46.67))\\\\=P(Z>1.50)\\\\=1-P(Z<1.50)\\\\=1-0.93319\\\\=0.06681\\\\\approx 0.0668`

Thus, the probability that he will earn at least $600 is 0.0668.

(b)

Let x represents his earnings on the best 1% of such weekends.

That is, P (X < x) = 0.99.

⇒ P (Z < z) = 0.99

The corresponding z-score is, 2.33.

Compute the value of x as follows:

`z=(S-\mu_(S))/(\sigma_(S))\\\\2.33=(x-530)/(46.67)\\\\x=530+(2.33* 46.67)\\\\x=638.7411\\\\x\approx 638.74`

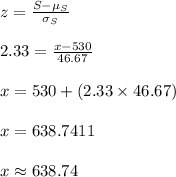
Thus, on the best 1% of such weekends the waiter earned $638.74.