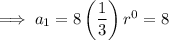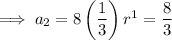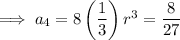Answer:
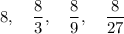
Explanation:
Sum to infinity of a geometric series:

Given:
 = 8
= 8
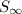 = 12
= 12
Substitute given values into the formula and solve for
 :
:
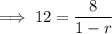

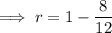
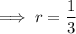
General form of a geometric sequence:

(where a is the first term and r is the common ratio)
Substitute the found values of
 and
and
 :
:
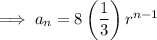
The first 4 terms: