Question

asked Sep 19, 2021 120k views

1 Answer

IlyaDoroshin · Answer 1 · 2021-09-25T12:45:57+0000

Explanation:

Point slope-form of a line passing through the point
(x_0, y_0) and having m is
$y-y_0=m(x-x_0)\cdots(i)$

The slope-intercept form of a line having slope m and y-intercept c is

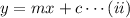
$y=mx+c\cdots(ii)$

(1). The line is passing through
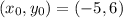(x_0, y_0)=(-5,6) and having the slope m=3.

So, by using equation (i), the point-slope form of the line is

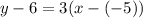
y-6=3(x-(-5))

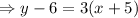
$\Rightarrow y-6=3(x+5)$

By using equation (ii), the slope-intercept form of the line is

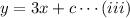
$y=3x+c\cdots(iii)$

as the line is passing through the point (-5,6), so pout this point in the equation (iii) to get the value of c.

6=3*(-5)+c

$\Rightarrow 6=-15+c$

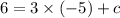
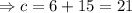
$\Rightarrow c=6+15=21$

From equation (iii), the slope-intercept form of the line is
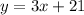y=3x+21 .

(2). The line is passing through the points (–5, 9) and (1, 3).

As two points are given, so the slope of the line is

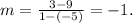
m=(3-9)/(1-(-5))=-1.

Now, proceeding in the same way as in part (1),

By using equation (i), the point-slope form of the line is

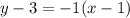y-3=-1(x-1) [taking point (1,3) and m=-1]

By using equation (ii), the slope-intercept form of the line is

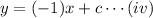
$y=(-1)x+c\cdots(iv)$

as the line is passing through the point (1,3), so pout this point in the equation (iv) to get the value of c.

3=-1*1+c

$\Rightarrow 3=-1+c$

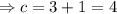
$\Rightarrow c=3+1=4$

From equation (iv), the slope-intercept form of the line is y=-x+4.

Please log in or register to add a comment.