Answer:
Mean
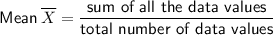
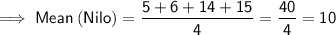
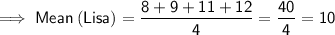
Standard Deviation
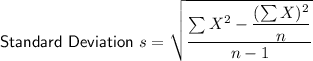

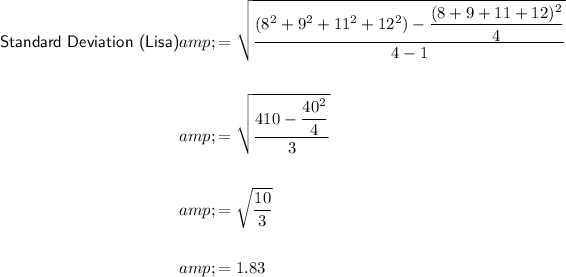
Summary
Nilo has a mean score of 10 and a standard deviation of 5.23.
Lisa has a mean score of 10 and a standard deviation of 1.83.
The mean scores are the same.
Nilo's standard deviation is higher than Lisa's. Therefore, Nilo's test scores are more spread out that Lisa's, which means Lisa's test scores are more consistent.