Question

A rectangular yard has a width that is 10 feet longer than the width . If the the area of the yard is 600 squared feet , find the dimension of the yard

Answer 1

length = 30 feet and width = 20 feet

Explanation:

Let l is length and b is width of a rectangular yard. The area of a rectangle is given by :

A = lb ..(1)

A rectangular yard has a length that is 10 feet longer than the width.

length, l = 10+b ...(2)

ATQ,

Put the value of l in equation (1),

`(10+b)b=600\\\\10b+b^2=600\\\\b^2+10b-600=0\\\\b^2+30b-20b-600=0\\\\b(b+30)-20(b+30)=0\\\\(b+30)(b-20)=0\\\\b=-30\ \text{feet}\ \text{and}\ b=20\ \text{feet}`

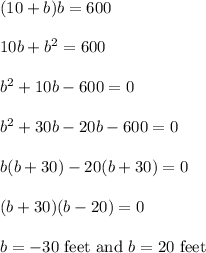
Width can't be negative. The width is 20 feet.

Put the value of b is equation (2),

l = 10+20

l = 30 feet

Hence, the length and width are 30 feet and 20 feet.