Answer:
x = -3
OR
x = -(3/5)
Step by step explanation:
Given:
To Find:
Soln:
Use quadratic formulae:
- Here I typed Quadratic formula as x
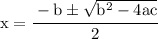
According to the question,on the formula,
So substitute them on the formula:
THEN solve for x.
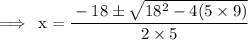
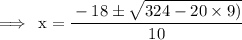
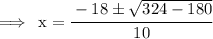
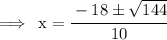
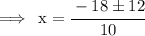
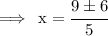
Final solution will after adding first(9+6),then secondly subtracting both 9-6
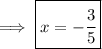
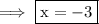
So there'll be two possible answers.