Question

1. Find the distance from point P to QS

SHOW ALL OF YOUR WORK

S(0,8)
R(-3,5)
Q(-5,3)
P(1, 1)

Answer 1

5.7 units

Explanation:

The distance from point P to QS is the distance from point P (1, 1) to the point of interception R(-3, 5).

Use distance formula to calculate distance between P and R:

`PR = √((x_2 - x_1)^2 + (y_2 - y_1)^2)`

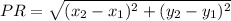
Let,

`P (1, 1) = (x_1, y_1)`

`R(-3, 5) = (x_2, y_2)`

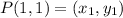
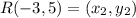
Plug in the values into the formula.

`PR = √((-3 - 1)^2 + (5 - 1)^2)`

`PR = √((-4)^2 + (4)^2)`

`PR = √(16 + 16)`

`PR = √(32)`

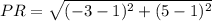
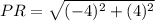
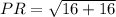
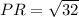
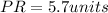`PR = 5.7 units` (to nearest tenth)