Question

In the right ∆ABC, BL is an angle bisector. If LB = 1.2 in and LC = 0.6 in. Find:

- The distance from L to AB.

- m∠ABC

Answer 1

Distance of L from AB = 0.6 in.

m∠ABC = 60°

Explanation:

Given:

LB = 1.2 in

LC = 0.6 in

We have to find the distance of point L to AB or length of LD.

From right triangle ΔBCL,

Sin(∠LBC) =
`\frac{\text{Opposite side}}{\text{Hypotenuse}}`

=
`(LC)/(LB)`

=
`(0.6)/(1.2)`

=
`(1)/(2)`

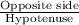
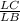
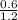
m∠LBC = 30° [Since ∠LBC is an acute angle]

Since, ∠LBC ≅ ∠LBA

m∠LBA = 30°

Now from right triangle ΔLDC,

sin(∠LBA) =
`(LD)/(BL)`

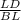
sin(30)° =
`(LD)/(1.2)`

`(1)/(2)=(LD)/(1.2)`

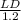
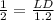
LD = 0.6

Therefore, Distance of point L from AB is 0.6 in.

m∠ABC = m∠ABL + m∠LBC

= 30° + 30°

= 60°