Question

If a neutral atom with 88 electrons undergoes 2 rounds of beta minus decay, what will be the new element?

Answer 1

The new element will be thorium-226 (²²⁶Th).

Step-by-step explanation:

The beta decay is given by:

`^(A)_(Z)X \rightarrow ^(A)_(Z+1)Y + \beta^(-) + \bar{\\u_(e)}`

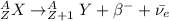
Where:

A: is the mass number

Z: is the number of protons

β⁻: is a beta particle = electron

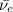`\bar{\\u_(e)}`: is an antineutrino

The neutral atom has 88 electrons, so:

`e^(-) = 88 = Z`

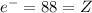
Hence the element is radium (Ra), it has A = 226.

If Ra undergoes 2 rounds of beta minus decay, we have:

`^(226)_(88)Ra \rightarrow ^(226)_(89)Ac + \beta^(-) + \bar{\\u_(e)}`

`^(226)_(89)Ac \rightarrow ^(226)_(90)Th + \beta^(-) + \bar{\\u_(e)}`

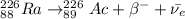
Therefore, if a neutral atom with 88 electrons undergoes 2 rounds of beta minus decay the new element will be thorium-226 (²²⁶Th).

I hope it helps you!