Question

Please help, I I beg you please

Answer 1

The volume of the cube is
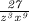`\mathit{(27)/(z^3x^(9))}` cu in.

Explanation:

The Volume of a Cube

Let's have a cube of side length a. The volume of the cube is:

`V=a^3`

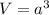
The cube of the image has a side length of

`\displaystyle a=(3x^(-3))/(z)\ inches`

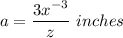
Simplifying the expression of the base by converting the negative exponent in the numerator to the denominator:

`\displaystyle a=(3)/(zx^(3))\ inches`

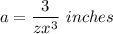
Now find the volume:

`\displaystyle V=\left((3)/(zx^(3))\ inches\right)^3`

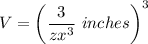
Applying the exponents:

`\displaystyle V=(3^3)/(z^3x^(9))\ inches^3`

`\displaystyle V=(27)/(z^3x^(9))\ inches^3`

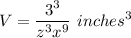
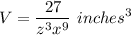
The volume of the cube is
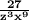`\mathbf{(27)/(z^3x^(9))}` cu in.