Answer:
The length of RS is 47 units
Explanation:
Midsegment Theorem
The midsegment of a trapezoid is a line segment that connects the midpoints of the non-parallel sides.
The length of the midsegment of a trapezoid is the average of the lengths of the bases.
The midsegment of the given trapezoid is VW, and the bases are RS and UT.
According to the midsegment theorem:
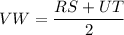
Substituting the variable lengths of the sides:
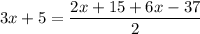
Operating:

Dividing the fraction:
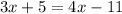
Rearranging:
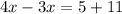
Operating:
x=16
The length of RS is:
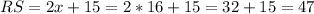
The lenght of RS is 47 units