Question

What is the equation of the circle with center (-3,1) that passes through the point (-5, 3)?

A)
(x - 3)2 + (y + 1)2 = 8
B)
(x + 3)2 + (y – 1)2 = 8
0)
(x + 1)2 – (y - 3)2 = 8
D)
(x + 3)2 - () - 1)2 = 8

Answer 1

Option B) (x + 3)^2 + (y – 1)^2 = 8 is the correct answer.

Explanation:

The equation of a circle with center (h,k) and radius r is given by:

`(x-h)^2 + (y-k)^2 = r^2`

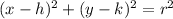
Given

Center = (h,k) = (-3,1)

=> h = -3

=> k = 1

The distance between the center of circle and the point through which the circle passes will be the radius.

The distance formula is given by:

`r = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2`

Given

`(x_1,y_1) = (-3,1)\\(x_2,y_2) = (-5,3)`

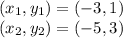
Putting the values in the formula

`r = √((-5+3)^2+(3-1)^2)\\r = √((-2)^2+(2)^2)\\r = √(4+4)\\r = √(8)`

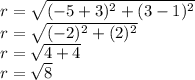
Putting the values of h,k and r in general form of equation

`\{x-(-3)}^2\} +(y-1)^2 = (√(8))^2\\(x+3)^2+(y-1)^2 = 8`

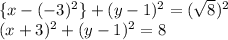
Hence,

Option B) (x + 3)^2 + (y – 1)^2 = 8 is the correct answer.