Question

The sum of the digits of a two-digit number is 8. The difference between the number and the reversed number is 10 more than the reversed number. Find the number.

Answer 1

The number is 62

Explanation:

Let the digits of the number be T and U;

A 2 digit number is represented as: 10T + U

So,

`T + U = 8`

`10T + U - (10U + T) = 10 + 10U + T`

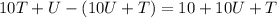
Required

Find the digit

Make U the subject in the first equation

`U = 8 - T`

Substitute 8 - T for U in the second

`10T + U - (10U + T) = 10 + 10U + T`

`10T + 8 - T - (10*(8-T) + T) = 10 + 10(8 - T) + T`

`10T + 8 - T - (80-10T + T) = 10 + 80 - 10T+ T`

`10T + 8 - T -80+10T - T = 10 + 80 - 10T+ T`

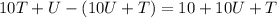
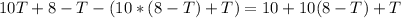
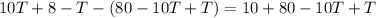
Collect Like Terms

`10T + 10T - T- T + 8 -80 = 10 + 80 - 10T+ T`

`18T -72 = 90 - 9T`

`9T + 18T = 90 + 72`

`27T = 162`

`T = 162/27`

`T = 6`

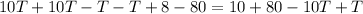
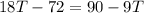
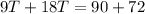
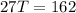
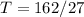
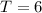
Recall that:

`U = 8 - T`

`U = 8 - 6`

`U = 2`

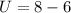
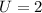
Hence, the number is 62