Question

The town of gettysburg, PA, plans to shoot a live cannon as part of their annual Gettysburg Civil War Battle Reenactment. The organizers want to make sure that when they fire the cannon, it lands in a location that does not injure any participants or spectators. The slope of the field they are firing into can be represented by the equation y=0.15x. Let x represent horizontal distance, and y represents vertical distance.. if the cannon fires the cannon ball at an arc denoted by the equation y=-0.5x^2+2.5x+1, at what distance will the cannonball land.

-I know i'm supposed to set -0.5x^2+2.5x+1=.15x and use distance formula BUT I KEEP GETTING DIFFERENT ANSWERS.

Answer 1

The cannonball lands at approximately 5.093 unit distance from the point of fire

Explanation:

The given parameters are;

The arc denoting the equation of motion of the cannon is y₁ = -0.5·x² + 2.5·x + 1

The slope of the field where in the direction the cannon is fired is y₂ = 1.5·x

The points where the cannonball land on the slopping field is given as rightly pointed by equating the two equations, the cannonball path path and the field path as follows;

At the point of contact of the cannonball and the field, the y-values of both equation will be equal

y₁ = y₂

∴ -0.5·x² + 2.5·x + 1 = 0.15·x

Which gives;

-0.5·x² + 2.5·x - 0.15·x + 1 = 0

-0.5·x² + 2.35·x + 1 = 0

-(-0.5·x² + 2.35·x + 1) = 0.5·x² - 2.35·x - 1 = 0

0.5·x² - 2.35·x - 1 = 0

The above equation is in the general form of a quadratic equation, which is given as follows;

a·x² + b·x + c = 0

By the quadratic equation, we have;

`x = \frac{-b\pm \sqrt{b^(2)-4\cdot a\cdot c}}{2\cdot a}`

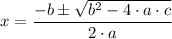
Plugging in the values, gives;

`x = \frac{2.35\pm \sqrt{(2.35)^(2)-4\cdot (0.5)* (-1)}}{2\cdot (0.5)} = (2.35\pm √(7.5225))/(1) =2.35 \pm √(7.5225)`

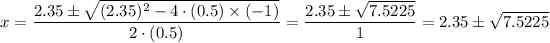
∴ x ≈ 5.093 or x ≈ -0.393

Therefore, the cannonball will takeoff at x ≈ -0.393 and land at x ≈ 5.093

The height from which they fire the cannon is given by the substituting the value of x ≈ -0.393 into the equation for the path of the cannonball, to give;

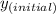`y_((initial))` = -0.5·(-0.393)² + 2.5·(-0.393) + 1 = -0.0597

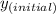`y_((initial))` ≈ -0.0597.

However, the actual initial height from which the cannonball is fired given by placing x = 0, which gives y = 1, which is the reason for the other (negative) value for x. Please see the attached graph created with Microsoft Excel.