Answer:
Given function:
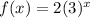
Part A
The average rate of change of function f(x) over the interval a ≤ x ≤ b is given by:
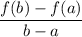
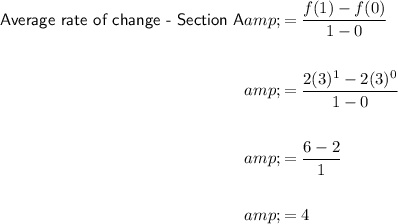
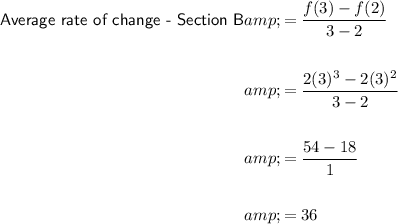
Part B
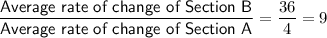
Therefore, the average rate of change of Section B is 9 times greater than Section A.
The function is an exponential function (with 3 as the growth factor) so the rate of change increases over time.