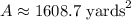Question

Please help me find the area of this!!! 15 points!!

Answer 1

`A\approx1608.7\text{ yards}^2`

Explanation:

We can use the alternate formula for the area of a triangle:

`A=(1)/(2)ab\sin(C)`

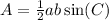
Where a and b are the side lengths, and C is the angle between the side lengths.

We know that one side length is 60 and the other is 70.

The angle between them is 50°.

So, substitute 60 for a, 70 for b, and 50° for C. This yields:

`A=(1)/(2)(60)(70)\sin(50)`

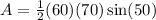
Evaluate using a calculator. Make sure you’re in Degrees Mode.

Therefore, the approximate area is:

`A\approx1608.7\text{ yards}^2`