Question

one line passes through (-3, -1) and (2,4) another passes through points (2, -6) and (7, -1). are the lines parallel, perpendicular, or neither?

Answer 1

Parallel

Explanation:

(-3, -1) and (2,4) -

First find the slope of the line using the slope formula
`(y2-y1)/(x2-x1)` :
`(4-(-1))/(2-(-3))`

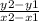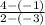
Add the numbers :
`(5)/(5)`

Simplify: 1

Using one of the given ordered pairs find the y-intercept: 4 = 1(2) + b

Caluclate the product : 4 = 2 + b

Move the variable to the left-hand side and change its sign: -b = 2 - 4

Calulate the diffrence and change the signs: b = 2

Using the slope and y- intersept creat your equation : y = 1x + 2

(2, -6) and (7, -1)-

First find the slope of the line using the slope formula
`(y2-y1)/(x2-x1)` :
`(-1-(-6))/(7-2)`

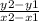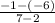
Add the numbers :
`(5)/(5)`

Simplify: 1

Using one of the given ordered pairs find the y-intercept: -6 = 1(2) + b

Caluclate the product : -6 = 2 + b

Move the variable to the left-hand side and change its sign: -b -6 = 2

Calulate the sum and change the signs: b = -8

Using the slope and y- intersept creat your equation : y = 1x + -8

Parallel lines have the same slope and different y-intercepts

Answer 2

Since they both have the same slope, they are Parallel.

Explanation:

We will have to calculate slope for this equation using this formula:

`(y2-y1)/(x2-x1)`

For line 1 our points are:

(-3,-1) and (2,4)

Substitute:

`(4+1)/(2+3)`

`(5)/(5)`

The slope for the first line is 1.

For line 2 our points are:

(2,-6) and (7,-1)

Substitute:

`(-1+6)/(7-2)`

`(5)/(5)`

The slope for this equation is 1.

For these lines to be parallel, they would need their slopes to be the same.

For these lines to be perpendicular, they would need to be opposite reciprocals.

Since they both have the same slope, they are Parallel.