Answer:
The vertex form of y = x² + 24x - 15 is y = (x + 12)² - 159
Explanation:
The vertex form of the quadratic equation y = ax² + bx + c is
y = a(x - h)² + k, where
- a is the coefficient of x²
- (h, k) are the coordinates of the vertex point
- h =
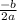 , where b is the coefficient of x
, where b is the coefficient of x
Let us use the facts above to solve the question
∵ y = x² + 24x - 15
∵ a is the coefficient of x² and b is the coefficient of x
∴ a = 1 and b = 24
∵ h is the x-coordinate of the vertex point
∵ h =
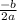
→ Substitute the values of a and b to find h
∴ h =
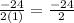
∴ h = -12
→ To find k substitute y by k and x by h
∵ y = k and x = h
∴ k = (-12)² + 24(-12) - 15 = 144 - 288 - 15
∴ k = -159
∴ The coordinates of the vertex point are (-12, -159)
→ Substitute the values of a, h, and k in the vertex form above
∵ y = 1(x - -12)² + (-159)
→ Remember (-)(-) = (+) and (+)(-) = (-)
∴ y = (x + 12)² - 159
∴ The vertex form of y = x² + 24x - 15 is y = (x + 12)² - 159