Question

Suppose you found a material in which 12.5% of the original radioactive atoms were present. If the half-life is 10years, how old is the material?

Answer 1

The material is 30 years old.

Step-by-step explanation:

The decay of radioactive isotopes can be modelled by the following ordinary differential equation:

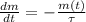`(dm)/(dt) = -(m(t))/(\tau)` (Eq. 1)

Where:

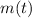`m(t)` - Current mass of the isotope, measured in grams.

`\tau` - Time constant, measured in years.

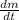`(dm)/(dt)` - Rate of change of the isotope in time, measured in grams per year.

After some handling, we find that the solution of the differential equation is:

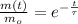`(m(t))/(m_(o)) = e^{-(t)/(\tau) }` (Eq. 2)

Where:

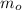`m_(o)` - Initial mass of the isotope, measured in grams.

`t` - Time, measured in years.

Now we clear time within the expression above:

`t = -\tau\cdot \ln (m(t))/(m_(o))`

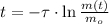
Besides, we determine the time constant in terms of the half-life (
`t_(1/2)`), measured in years:

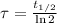`\tau = (t_(1/2))/(\ln 2)` (Eq. 3)

If we know that
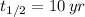`t_(1/2) = 10\,yr` and
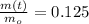`(m(t))/(m_(o)) = 0.125`, then the age of the material is:

`\tau = (10\,yr)/(\ln 2)`

`\tau = 14.427\,yr`

`t = -(14.427\,yr)\cdot \ln 0.125`

`t \approx 30\,yr`

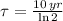
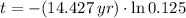
The material is 30 years old.