Question

What is the solution to the inequality below? 2(x -1) - 4(x + 2) < 5x

Answer 1

`\boxed {x > -(10)/(7)}`

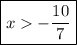
Explanation:

Solve the given inequality:

`2(x - 1) - 4(x + 2) < 5x`

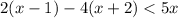
-Use Distributive Property:

`2(x - 1) - 4(x + 2) < 5x`

`2x - 2 - 4x - 8 < 5x`

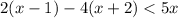
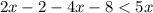
-Combine like terms:

`2x - 2 - 4x - 8 < 5x`

`-2x - 10 < 5x`

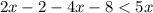
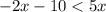
-Subtract both sides by
`5x`:

`-2x - 10 - 5x < 5x - 5x`

`-7x - 10 < 0`

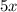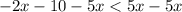
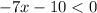
-Add both sides by
`10`:

`-7x - 10 + 10 < + 10`

`-7x < 10`

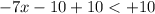
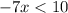
-When you are dividing a integer by a negative integer, the inequality sign would change. So, divide both sides by
`-7`:

`(-7x)/(-7) < (10)/(-7)`

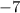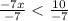
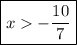`\boxed {x > -(10)/(7)}` (final answer)