Answer:
Function B has the greater rate of change, and Function A has the greater y-intercept
Explanation:
Equation representing Function A: y= 3/4x + 2
Where,
slope/rate of change (m) = ¾
y-intercept (b) = 2
Using the graph given for Function B, let's find an equation for Function B by determining the slope of the line/rate of change (m) and y-intercept (b).
Using points (1, 0) and (2, 2), which are two points on the line, find slope (m), which is also represents the rate of change.
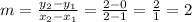
Rate of change for function B (m) = 2
y-intercept (b) is the point at which the y-axis is intercepted by the line of the graph = -2
Substitute, m = 2, and b = -2 into y = mx + b.
The equation for Function B would be:
y = 2x +(-2)
y = 2x - 2.
slope/rate of change (m) = 2
y-intercept (b) = -2
Comparing the Function A and Function B,
Function A rate of change is ¾, while that of B is 2. Therefore, Function B has the greater rate of change.
Function A has y-intercept of 2, while Function B has a y-intercept of -2. Therefore, Function A has the greater y-intercept.