Question

An airplane flies from City 1 at (0, 0) to City 2 at (33, 56) and then to City 3 at (23, 32). What is the total number of miles it flies? Each unit represents 1 mile.

Answer 1

Question:

An airplane flies from City 1 at (0, 0) to City 2 at (33, 56) and then to City 3 at (23, 32). What is the total number of miles it flies? Each unit represents 1 mile.

Answer:

The plane flew 91 miles.

Explanation:

City 1 - City 2

---------------------------------------------------------------------------------------------------------

`d_(1)` =
`\sqrt{(33 - 0)^(2) + (56 - 0)^(2)`

`d_(1)` =
`\sqrt{33^(2) + 56^(2)`

`d_{1` =
`\sqrt{1089 + 3136`

`d_(1)` =
`√(4225)`

`d_1` =
`65`

---------------------------------------------------------------------------------------------------------

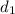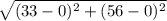
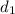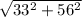
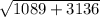
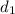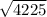
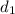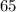
City 2 - City 3

`d_2` =
`\sqrt{(33 - 23)^2 + (56 - 32)^2`

`d_2` =
`\sqrt {10^2 + 24^2}`

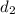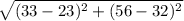
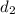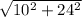
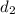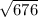
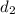`d_2` =
`√(676)`

`d_2` = 26

---------------------------------------------------------------------------------------------------------

`d_1 + d_2 = 65 + 26`

`d_1 + d_2 = 91`

---------------------------------------------------------------------------------------------------------

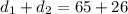
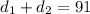
Therefore, the airplane flew a total of 91 miles through every city

---------------------------------------------------------------------------------------------------------

Key words: the airplane, 91 miles, through, every, city, flies, City 1, City 2, City 3, total, number, unit, represent, mile.

<3 Lots of love!

-The Book Worm.

Answer 2

The airplane flies 95 miles.

Explanation:

1. First we need to find the distance for the first segment using the formula for distance
   `D=\sqrt{(x_(2)-x_(1))^2 + (y_(2)-y_(1))^2}`. Let's say
   `(x_(1),y_(1))` is (0, 0) and
   `(x_(2),y_(2))` is (33, 56). This gets us that the length of this segment is 65 miles.
2. Next, we need to find the distance for the second segment. Using the same formula for distance
   `D=\sqrt{(x_(2)-x_(1))^2 + (y_(2)-y_(1))^2}`, we can say
   `(x_(1),y_(1))` is now (33, 56) and
   `(x_(2),y_(2))` is now (23, 32). This gets us that the length of this segment is 26 miles.
3. To get the total distance traveled, add the length of these two segments together (65 miles + 26 miles) to get 91 total miles traveled.