Check the picture below.
![~\hfill \stackrel{\textit{\large distance between 2 points}}{d = √(( x_2- x_1)^2 + ( y_2- y_1)^2)}~\hfill~ \\\\[-0.35em] ~\dotfill\\\\ Q(\stackrel{x_1}{-4}~,~\stackrel{y_1}{9})\qquad U(\stackrel{x_2}{2}~,~\stackrel{y_2}{3}) ~\hfill QU=√([ 2- (-4)]^2 + [ 3- 9]^2) \\\\\\ ~\hfill \boxed{QU=√(72)} \\\\\\ U(\stackrel{x_1}{2}~,~\stackrel{y_1}{3})\qquad A(\stackrel{x_2}{-3}~,~\stackrel{y_2}{-2}) ~\hfill UA=√([ -3- 2]^2 + [ -2- 3]^2) \\\\\\ ~\hfill \boxed{UA=√(50)}](https://img.qammunity.org/2023/formulas/mathematics/college/ff7mfl9s6y0tnqui5t1ibcotufqwq2luut.png)
![A(\stackrel{x_1}{-3}~,~\stackrel{y_1}{-2})\qquad D(\stackrel{x_2}{-9}~,~\stackrel{y_2}{4}) ~\hfill AD=√([ -9- (-3)]^2 + [ 4- (-2)]^2) \\\\\\ ~\hfill \boxed{AD=√(72)} \\\\\\ D(\stackrel{x_1}{-9}~,~\stackrel{y_1}{4})\qquad Q(\stackrel{x_2}{-4}~,~\stackrel{y_2}{9}) ~\hfill DQ=√([ -4- (-9)]^2 + [ 9- 4]^2) \\\\\\ ~\hfill \boxed{DQ=√(50)}](https://img.qammunity.org/2023/formulas/mathematics/college/dgpyx6rvfebtkhuqwkype9embk6ugr0pv7.png)
now, let's take a peek at that above, DQ = UA and QU = AD, so opposite sides of the polygon are equal.
Now, let's check the slopes of DQ and QU
![D(\stackrel{x_1}{-9}~,~\stackrel{y_1}{4})\qquad Q(\stackrel{x_2}{-4}~,~\stackrel{y_2}{9}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{9}-\stackrel{y1}{4}}}{\underset{run} {\underset{x_2}{-4}-\underset{x_1}{(-9)}}} \implies \cfrac{9 -4}{-4 +9}\implies \cfrac{5}{5}\implies \cfrac{1}{1}\implies 1 \\\\[-0.35em] ~\dotfill](https://img.qammunity.org/2023/formulas/mathematics/college/szceesh05pplmq5nwkof3m2ppygc0x4z8t.png)
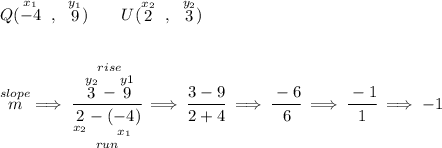
keeping in mind that perpendicular lines have negative reciprocal slopes, let's notice that the reciprocal of 1/1 is just 1/1 and the negative of that is just -1/1 or -1, so QU has a slope that is really just the negative reciprocal of DQ, those two lines are perpendicular, thus making a 90° angle, and their congruent opposite sides will also make a 90°, that makes QUAD hmmm yeap, you guessed it.