Answer:
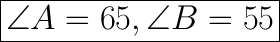
Explanation:
We can treat each of these angle equations as if they are the real angle measures.
We know these angles add up to 120°, so we can create an addition statement:
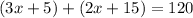
We can then solve for x.
- Combine like terms:
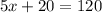
- Subtract 20 from both sides:
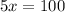
- Divide both sides by 5:
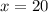
Now that we know x = 20, we can substitute it into both equations for each angles and find it.
∠A =
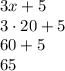
∠B =
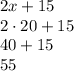
We can test that this is right because 65+55 = 120.
Hope this helped!