Question

Please Show Work.

The measure of angles in a triangle are in a ratio of 2:3:4. What are the measures of the angles?

Answer 1

The angle measures are 40°, 60°, and 80°.

Explanation:

When we are given this problem, we need to know that

• There are three angles in a triangle.
• These angles add up to equal 180°.

With this ratio, these angles must add up to equal 180°. Therefore, we can set up an equation and add an x-variable to each of the numbers. We then set this equal to 180.

`\text{2x + 3x + 4x = 180}\\\\\text{9x = 180}\\\\\text{x = 20}`

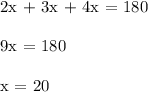
Now, we need to find the measures of the angles. The angles are the parts of the ratio multiplied by the value of x.

`\text{2(20) = 40}\\\\\text{3(20) = 60}\\\\\text{4(20) = 80}`

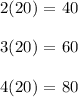
So, our three angles measures should be 40°, 60°, and 80°. We can check this by adding up these three values and seeing if the sum equals 180°.

`\text{40 + 60 + 80 = 180}\\\\\text{100 + 80 = 180}\\\\\text{180 = 180}`

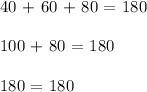
Because this is true, our angle measures are 40°, 60°, and 80°.