Given:
V'W'X'Y' has vertices V'(-3,2), W'(5,1), X'(0,4) and Y'(-2,0).
V'W'X'Y' is the image of VWXY rotated 90° around the origin.
To find:
The coordinates of VWXY (the pre-image).
Solution:
V'W'X'Y' is the image of VWXY rotated 90° around the origin. It means, the figure VWXY is rotated 90° counterclockwise around the origin.
So, if we rotate V'W'X'Y' 90° clockwise around the origin, then we get the original figure VWXY.
If a figure rotated 90° clockwise around the origin, then
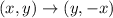
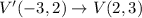
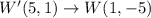
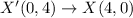
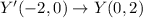
Therefore, the coordinates of preimage are V(2,3), W(1,-5), X(4,0) and Y(0,2).