Question

Given the vertex: (-5, -3) and a point from the graph: (-4, —5), write the

equation of the parabola in Vertex Form.

Answer 1

`y=-2(x+5)^2-3`

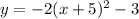
Explanation:

Equation of the Quadratic Function

The vertex form of the quadratic function has the following equation:

`y=a(x-h)^2+k`

Where (h, k) is the vertex of the parabola that results when plotting the function, and a is a coefficient different from zero.

The given vertex is (-5,-3), thus:

`y=a(x-(-5))^2-3`

`y=a(x+5)^2-3`

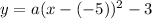
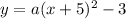
We need to find the value of a. We use the point (-4,-5):

`-5=a(-4+5)^2-3`

`-5=a(1)^2-3`

`-5=a-3`

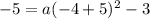
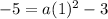
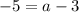
Solving:

`a=-5+3=-2`

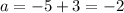
The complete equation of the parabola is:

`\mathbf{y=-2(x+5)^2-3}`