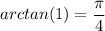Question

Explain why arctan(1) = 45° or π/4.

Answer 1

Explanation below

Explanation:

Inverse Trigonometric Functions

They are defined as the inverse of the basic trigonometric functions which are sine, cosine, tangent, cotangent, secant, and cosecant.

The corresponding inverse functions are called arcsin, arccos, arctan, arccot, arcsec, arccsc.

These inverse functions in trigonometry are used to get the angle with any of the trigonometry ratios.

For example,

`\displayystyle \sin 30^\circ=(1)/(2)`

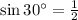
Then:

`\displaystyle arcsin (1)/(2)=30^\circ`

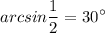
Since:

`\tan 45^\circ=1`

Or, equivalently:

`\displaystyle \tan (\pi)/(4)=1`

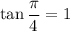
Then:

`\displaystyle arctan(1)=45^\circ`

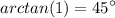
Or:

`\displaystyle arctan(1)=(\pi)/(4)`