Question

A 20 gram bullet exits the rifle at a speed of 985 m/s. the gun barrel is 0.8 m long. what

was the force during the rocket's launch?

Answer 1

Hello!

We can use the following relationship:

`\Delta KE = W = F \cdot d`

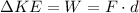
ΔKE = Change in Kinetic Energy (J)
W = Work done on object (J)

F = Force (N)

d = distance of which the force is applied to the object. (This is equivalent to the length of the gun barrel, or 0.8 m)

Also, recall that:

`KE = (1)/(2)mv^2`

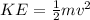
m = mass of bullet (0.02 kg)

v = velocity of bullet (vfinal = 985 m/s, vinitial = 0 m/s)

We can now solve.

`\Delta KE = F \cdot d\\\\KE_f - KE_i = F \cdot d\\\\(1)/(2)(0.02)(985^2) - (1)/(2)(0.02)(0^2) = (0.8)F\\\\9702.25 = 0.8F\\\\F = (9702.25)/(0.8) = \boxed{12127.813 N}`