Question

Basic Computation: Find Probabilities In Problems 5-14, assume that x has a normal distribution with the specified mean and standard deviation. Find the indicated probabilities. P(3 lessthanorequalto x lessthanorequalto 6)

: mu = 4: sigma = 2 P(50 lessthanorequalto x lessthanorequalto 70)
: mu = 40: sigma = 15 P(8 lessthanorequalto x lessthanorequalto 12)
: mu = 15: sigma = 3.2 P(x greaterthanorequalto30)
: mu = 20: sigma = 3.4 P(x greaterthanorequalto90)
: mu = 100: sigma = 15 P(10 lessthanorequalto x lessthanorequalto 20)
: mu = 15: sigma = 4 P(7 lessthanorequalto x lessthanorequalto 9)
: mu = 5: sigma = 1.2 P(40 lessthanorequalto x lessthanorequalto 47)
: mu = 50: sigma = 15 p(x greaterthanorequalto 120)
: mu = 10: sigma = 15 P(x greaterthanorequalto 2)
: mu = 3
: sigma = 0.25

Answer 1

the answer is below

Explanation:

The z score is used to calculate by how many standard deviations the raw score is above or below the mean. The z score is given as:

`z=(x-\mu)/(\sigma)\\\\\mu=mean,\sigma=standard\ deviation`

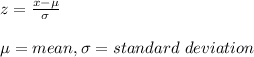
1) For x = 3

`z=(x-\mu)/(\sigma)=(3-4)/(2)=-0.5`

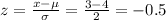
For x = 6

`z=(x-\mu)/(\sigma)=(6-4)/(2)=1`

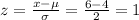
P(3 ≤ x ≤ 6) = P(-0.5 ≤ z ≤ 1) = P(z < 1) - P(z < -0.5) = 0.8413 - 0.3085 = 0.5328

2) For x = 50

`z=(x-\mu)/(\sigma)=(50-40)/(15)=0.67`

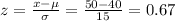
For x = 70

`z=(x-\mu)/(\sigma)=(70-40)/(15)=2`

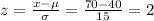
P(50 ≤ x ≤ 70) = P(0.67 ≤ z ≤ 2) = P(z < 2) - P(z < 0.67) = 0.9772 - 0.7486 = 0.2286

3) For x = 8

`z=(x-\mu)/(\sigma)=(8-15)/(3.2)=-2.19`

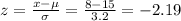
For x = 12

`z=(x-\mu)/(\sigma)=(12-15)/(3.2)=-0.94`

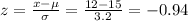
P(8 ≤ x ≤ 12) = P(-2.19 ≤ z ≤ -0.94) = P(z < -0.94) - P(z < -2.19) = 0.1736 - 0.0143 = 0.1593

4) For x = 30

`z=(x-\mu)/(\sigma)=(30-20)/(3.4)=2.94`

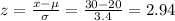
P(x ≥ 30) = P(z ≥ 2.94) = 1 - P(z < 2.94) = 1 - 0.9984 = 0.0016

5) x = 90

`z=(x-\mu)/(\sigma)=(90-100)/(15)=-0.67`

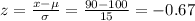
P(x ≥ 90) = P(z ≥ -0.67) = 1 - P(z < -0.67) = 1 - 0.2514 = 0.7486

6) For x = 10

`z=(x-\mu)/(\sigma)=(10-15)/(4)=-1.25`

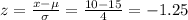
For x = 20

`z=(x-\mu)/(\sigma)=(20-15)/(4)=1.25`

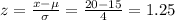
P(10 ≤ x ≤ 20) = P(-1.25 ≤ z ≤ 1.25) = P(z < 1.25) - P(z < -1.25) = 0.8944 - 0.1056 = 0.7888

7) For x = 7

`z=(x-\mu)/(\sigma)=(7-5)/(1.2)=1.67`

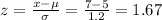
For x = 9

`z=(x-\mu)/(\sigma)=(9-5)/(1.2)=3.33`

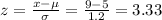
P(7 ≤ x ≤ 9) = P(1.67 ≤ z ≤ 3.33) = P(z < 3.33) - P(z < 1.67) = 0.9996 - 0.9525 = 0.0471

8) For x = 40

`z=(x-\mu)/(\sigma)=(40-50)/(15)=-0.67`

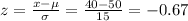
For x = 47

`z=(x-\mu)/(\sigma)=(47-50)/(15)=-0.2`

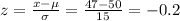
P(40 ≤ x ≤ 47) = P(-0.67 ≤ z ≤ -0.2) = P(z < -0.2) - P(z < -0.67) = 0.4207 - 0.2514 = 0.1693

9) x = 120

`z=(x-\mu)/(\sigma)=(120-10)/(15)=7.33`

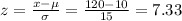
P(x ≥ 120) = P(z ≥ 7.33) = 1 - P(z < 7.33) = 1 - 0.9999 = 0.001

10) x = 2

`z=(x-\mu)/(\sigma)=(2-3)/(0.25)=-4`

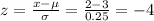
P(x ≥ 2) = P(z ≥ -4) = 1 - P(z < -4) = 1 - 0.0001 = 0.999