Question

In a power plant cycle 30 MW is taken out in the condenser, 21 MW is taken out in the turbine, and the pump work is 200 kW. Find the plant thermal efficiency. If everything could be reversed find the COP as a refrigerator

Answer 1

The thermal efficiency of the power plant cycle is 40.95 percent.

The COP as a refrigerator is 1.442.

Step-by-step explanation:

From Thermodynamics we get that thermal efficiency for power cycles is represented by the following definition:

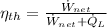`\eta_(th) = (\dot W_(net))/(\dot W_(net)+\dot Q_(L))` (Eq. 1)

Where:

`\dot W_(net)` - Net power of the power cycle, measured in kilowatts.

`\dot Q_(L)` - Heat rate released from condenser, measured in kilowatts.

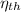`\eta_(th)` - Thermal efficiency of the power plant cycle, dimensionless.

The net power cycle is determined by the following expression:

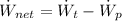`\dot W_(net) = \dot W_(t)-\dot W_(p)` (Eq. 2)

Where:

`\dot W_(t)` - Power generated by the turbine, measured in kilowatts.

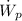`\dot W_(p)` - Power consumed by the pump, measured in kilowatts.

If we know that
`\dot W_(p) = 200\,kW`,
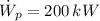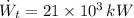`\dot W_(t) = 21* 10^(3)\,kW` and
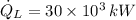`\dot Q_(L) = 30* 10^(3)\,kW`, then the thermal efficiency of the power plant cycle is:

`\dot W_(net) = 21* 10^(3)\,kW-200\,kW`

`\dot W_(net) = 20.8* 10^(3)\,kW`

`\eta_(th) = (20.8* 10^(3)\,kW)/(20.8* 10^(3)\,kW + 30* 10^(3)\,kW)`

`\eta_(th) = 0.409` (
`40.95\,\%`)

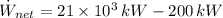
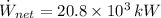
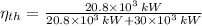
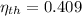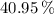The thermal efficiency of the power plant cycle is 40.95 percent.

For refrigeration cycles we remember that the Coefficient of Performance (
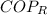`COP_(R)`), dimensionless, is represented by the following model:

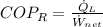`COP_(R) = (\dot Q_(L))/(\dot W_(net))` (Eq. 3)

If we know that
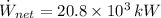`\dot W_(net) = 20.8* 10^(3)\,kW` and
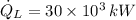`\dot Q_(L) = 30* 10^(3)\,kW`, then the Coefficient of Performance is:

`COP_(R) = (30* 10^(3)\,kW)/(20.8* 10^(3)\,kW)`

`COP_(R) = 1.442`

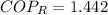
The COP as a refrigerator is 1.442.