Question

A sample of 40 individuals at a shopping mall found that the mean number of visits to a restaurant per week was 2.88 with a standard deviation of 1.59. Find a 99% confidence interval for the mean num-ber of restaurant visits. Use the appropriate formula and verify your result using the Confidence Intervals workbook.

Answer 1

The confidence interval is between 2.23 and 3.53

Step-by-step explanation:

The confidence interval (C) = 99% = 0.99

α = 1 - C = 1 - 0.99 = 0.01

α/2 = 0.01/2 = 0.005

The z score of α/2 corresponds to the z score of 0.495 (0.5 - 0.005) which is 2.576

The margin of error (E) is given as:

`E=z_{(\alpha)/(2) }*(\sigma)/(√(n) )\\\\where\ n=sample\ size,\sigma=standard\ deviation\\\\Given\ that\ \sigma=1.59,n=40,z_{(\alpha)/(2) }=2.576\ hence: \\\\E=2.576*(1.59)/(√(40) ) =0.65`

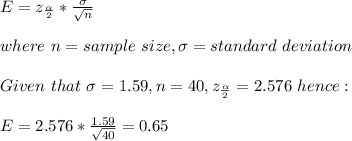
The confidence interval = mean ± margin of error = 2.88 ± 0.65 = (2.23, 3.53)

The confidence interval is between 2.23 and 3.53