Question

Suppose X has a continuous uniform distribution over the interval [1.3, 6.2]. Round your answers to 3 decimal places.

Required:
a. Determine the mean of X.
b. Determine the variance of X
c. What is P(X < 3.7)?

Answer 1

(a) 3.75

(b) 2.00083

(c) 0.4898

Explanation:

It is provided that X has a continuous uniform distribution over the interval [1.3, 6.2].

(a)

Compute the mean of X as follows:

`\mu_(X)=(a+b)/(2)=(1.3+6.2)/(2)=3.75`

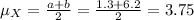
(b)

Compute the variance of X as follows:

`\sigm^(2)_(X)=((b-a)^(2))/(12)=((6.2-1.3)^(2))/(12)=2.00083`

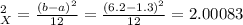
(c)

Compute the value of P(X < 3.7) as follows:

`P(X < 3.7)=\int\limits^(3.7)_(1.3){(1)/(6.2-1.3)}\, dx\\\\=(1)/(4.9)* [x]^(3.7)_(1.3)\\\\=(3.7-1.3)/(4.9)\\\\\approx 0.4898`

Thus, the value of P(X < 3.7) is 0.4898.