Question

The following are the annual salaries of 15 chief executive officers of major companies. (The salaries are written in thousands of dollars.)

157, 700, 1250, 767, 381, 495, 248, 75, 586, 224, 723, 472, 743, 676, 271


Required:
Find 25th and 70th percentiles for these salaries.

Answer 1

The 25th percentile is 248.

The 70th percentile is 700.

Explanation:

The pth percentile is a data value such that at least p% of the data-set is less-than or equal to this data value and at least (100-p)% of the data-set are more-than or equal to this data value.

Arrange the data set in ascending order as follows:

S = {75 , 157 , 224 , 248 , 271 , 381 , 472 , 495 , 586 , 676 , 700 , 723 , 743 , 767 , 1250}

The formula to compute the position of the pth percentile is:

`p^(th) \text{Percentile}=((n+1)\cdot p)/(100)`

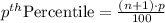
Compute the 25th percentile as follows:

`25^(th) \text{Percentile}=((15+1)\cdot 25)/(100)=4^(th)obs.`

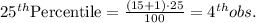
The 4th observation from the arranged data set is 248 .

Thus, the 25th percentile is 248.

Compute the 70th percentile as follows:

`70^(th) \text{Percentile}=((15+1)\cdot 70)/(100)\approx 11^(th)obs.`

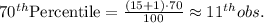
The 11th observation from the arranged data set is 700.

Thus, the 70th percentile is 700.