Answer:
0.8809
Explanation:
Given that:
The population proportion p = 4% = 4/100 = 0.04
Sample mean x = 16
The sample size n = 300
The sample proportion
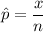
= 16/300
= 0.0533
∴
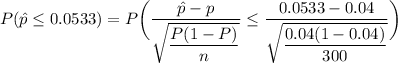
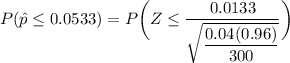
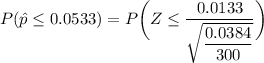
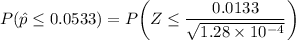
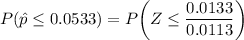
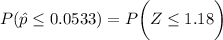
From the z tables;
= 0.8809
OR
Let X be the random variation that follows a normal distribution;
Then;
population mean
 = n × p
= n × p
population mean
 = 300 × 0.04
= 300 × 0.04
population mean
 = 12
= 12
The standard deviation
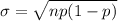
The standard deviation
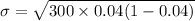
The standard deviation

The standard deviation
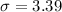
The z -score can be computed as:
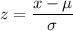

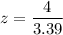
z = 1.18
The required probability is:
P(X ≤ 10) = Pr (z ≤ 1.18)
= 0.8809