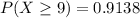Question

A manufacturer of televisions subjects the equipment to a comprehensive testing process for all essential functions before the television leaves the factory. If the probability of passing these comprehensive tests is 0.95 and if 10 televisions are randomly selected what is that probability that at least 9 pass the test?

Answer 1

The value is
`P(X \ge 9) = 0.9138`

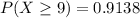
Explanation:

From the question we are told that

The probability of passing the test is
`p = 0.95`

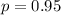
The sample size is n = 10

Generally the distribution of the comprehensive testing of equipment follows a binomial distribution

i.e

`X  \~ \ \ \  B(n , p)`

and the probability distribution function for binomial distribution is

`P(X = x) =  ^(n)C_x *  p^x *  (1- p)^(n-x)`

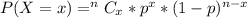
Here C stands for combination hence we are going to be making use of the combination function in our calculators

Generally the probability that at least 9 pass the test is mathematically represented as

`P(X \ge 9) = P(X = 9 ) + P(X = 10 )`

=>
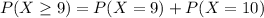
`P(X \ge 9) =  [^(10)C_9 *  (0.95)^9 *  (1- 0.95)^(10-9)] + [^(10)C_(10) *  (0.95)^(10) *  (1- 0.95)^(10-10)]`

=>
`P(X \ge 9) =  [0.3151] + [0.5987]`

=>
`P(X \ge 9) = 0.9138`