Question

A genetic experiment with peas resulted in one sample of offspring that consisted of 438 green peas and 173 yellow peas.

Required:
a. Construct a 95â% confidence interval to estimate of the percentage of yellow peas.
b. It was expected thatâ 25% of the offspring peas would be yellow. Given that the percentage of offspring yellow peas is notâ 25%, do the results contradictâ expectations?

Answer 1

a

The 95% confidence interval is
`0.2474 < p < 0.3188`

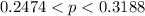
b

The result obtained does not contradict expectation

Explanation:

From the question we are told that

The number of green peas is k = 438

The number of yellow peas is u = 173

Generally the sample size is mathematically represented as

`n = k + u`

=>
`n = 438 + 173`

=>
`n = 611`

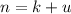
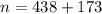
Generally the sample proportion for yellow peas is

`\^ p = (u)/(n)`

=>
`\^ p = (173)/(611 )`

=>
`\^ p = 0.2831`

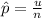
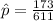
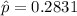
From the question we are told the confidence level is 95% , hence the level of significance is

`\alpha = (100 - 95 ) \%`

=>
`\alpha = 0.05`

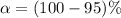
Generally from the normal distribution table the critical value of
`(\alpha )/(2)` is

`Z_{(\alpha )/(2) } =  1.96`

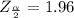
Generally the margin of error is mathematically represented as

`E =  Z_{(\alpha )/(2) } * \sqrt{(\^ p (1- \^ p))/(n) }`

=>
`E =  1.96 * \sqrt{( 0.2831 (1- 0.2831))/(611) }`

=>
`E =  0.0357`

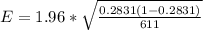
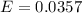
Generally 95% confidence interval is mathematically represented as

`\^ p -E <  p <  \^ p +E`

=>
`0.2831  -0.0357 <p< 0.2831  + 0.0357`

=>
`0.2474 < p < 0.3188`

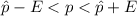
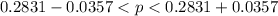
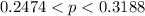
From the question we are told that it was expected that 25% of the offspring peas will be yellow

Now from the 95% confidence interval obtained we see that the expected sample proportion(25% ) falls within it so it means that the result obtained does not contradict expectation