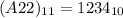Question

Compute the decimal representation for each of the following numbers.

a. (1100110)2
b. (346)7
c. (1024)8
d. (3B2)16
e. (AF72)16
f. (120121)3
g. (A22)11

Answer 1

`(1100110)_2= 102_{10`

`(346)_7= 181_{10`

`(1024)_8 = 532_{10`

`(3B2)_(16) = 946_{10`

`(AF72)_(16)= 44914_{10`

`(120121)_3= 421_{10`

`(A22)_(11) = 1234_(10)`

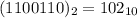
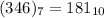
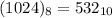
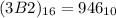
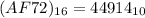
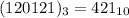
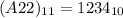
Step-by-step explanation:

Required

Convert to decimal

To do this we get the position of individual digits (starting from the rightmost digit).

Then each digit is multiplied by the base raise to power its position.

Lastly, we sum the results of the products.

Following the above steps, we have:

`a.\ (1100110)_2`

`= 1 * 2^6 + 1 * 2^5 + 0 * 2^4 + 0 * 2^3 + 1 * 2^2 + 1 * 2^1 + 0 * 2^0`

`= 1 * 64 + 1 * 32 + 0 * 16 + 0 * 8 + 1 * 4 + 1 * 2 + 0 * 1`

`= 64 + 32 + 0 + 0 + 4 + 2 + 0`

`= 102`

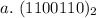
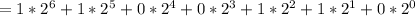
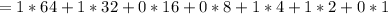
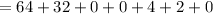
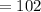
Hence:

`(1100110)_2= 102_{10`

`b.\ (346)_7`

`= 3 * 7^2 + 4*7^1 + 6 * 7^0`

`= 3 * 49 + 4*7 + 6 * 1`

`= 147 + 28 + 6`

`= 181`

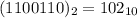
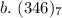
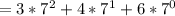
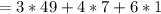
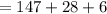
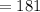
Hence:

`(346)_7= 181_{10`

`c.\ (1024)_8`

`= 1 * 8^3 + 0 * 8^2 + 2 * 8^1 + 4 * 8^0`

`= 1 * 512+ 0 * 64 + 2 * 8 + 4 * 1`

`= 512+ 0 + 16 + 4`

`= 532`

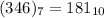
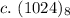
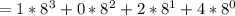
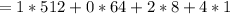
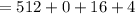
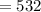
Hence:

`(1024)_8 = 532_{10`

`d.\ (3B2)_{16`

`= 3 * 16^2 + B * 16^1 + 2 * 16^0`

`= 3 * 256 + B * 16 + 2 * 1`

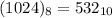
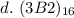
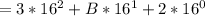
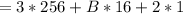
B represents 11, so we have:

`= 3 * 256 + 11 * 16 + 2 * 1`

`= 768 + 176 + 2`

`= 946`

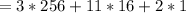
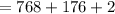
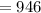
Hence:

`(3B2)_(16) = 946_{10`

`e.\ (AF72)_{16`

`= A * 16^3 + F * 16^2 + 7 * 16^1 + 2 * 16^0`

`= A * 4096 + F * 256 + 7 * 16 + 2 * 1`

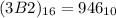
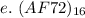
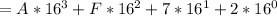
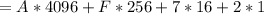
A represents 10 and F, 15; So, we have:

`= 10 * 4096 + 15 * 256 + 7 * 16 + 2 * 1`

`= 40960 + 3840 + 112 + 2`

`= 44914`

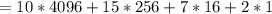
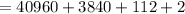
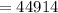
Hence:

`(AF72)_(16)= 44914_{10`

`f.\ (120121)_3`

`= 1 * 3^5 + 2*3^4 + 0*3^3 + 1*3^2 + 2*3^1 + 1*3^0`

`= 1 * 243 + 2*81 + 0*27 + 1*9 + 2*3 + 1*1`

`= 243 + 162 + 0 + 9 + 6 + 1`

`= 421`

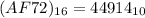
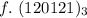
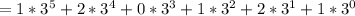
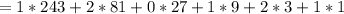
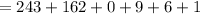
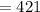
Hence:

`(120121)_3= 421_{10`

`g.\ (A22)_{11`

`= A * 11^2 + 2 * 11^1 + 2 * 11^0`

`= A * 121 + 2 * 11 + 2 * 1`

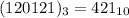
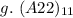
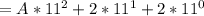
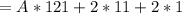
A represents 10, so we have:

`= 10 * 121 + 2 * 11 + 2 * 1`

`= 1210 + 22+ 2`

`= 1234`

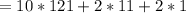
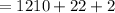
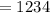
Hence:

`(A22)_(11) = 1234_(10)`