Question

In a game, you have a 1/21 probability of winning $107 and a 20/21 probability of losing $5. What is your expected winning?

A) $0.33
B) $9.86
C) $5.10
D) -$4.76

Answer 1

The correct option is A.

Explanation:

The formula to compute the expected value is:

`E(X)=\sum x\cdot P(X)`

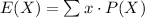
The information provided can be summarized as follows:

X P (X)

Win $107 1/21

Lose -$5 20/21

Compute the value of expected winning as follows:

`E(X)=\sum x\cdot P(X)`

`=(107*(1)/(21))+(-5*(20)/(21))\\\\=(107)/(21)-(100)/(21)\\\\=(107-100)/(21)\\\\=0.33333333\\\\\approx \$0.33`

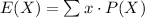
Thus, the value of expected winning is $0.33.

The correct option is A.