Question

The general solution to the second-order differential equation y″+6y′−40y=0 is in the form y(x)=c1er1x+c2er2x. Find the values of r1 and r2.

Answer 1

r1 = 4 and r2 = -10 and the final equation will be C1e^4x + C2e^-10x

Explanation:

The general solution to the second order differential equation

y'' + 6y' -40y=0

substitute y= e^rx

y' = re^rx

y'' = r^2*e^rx

The equation will be

r^2*e^rx + 6r*e^rx - 40*e^rx = 0

e^rx (
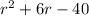`\\r^2 + 6r - 40`) = 0

Characteristic equation =
`\\r^2 + 6r - 40`

=
`r^2 +10r - 4r -40\\`

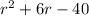
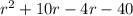
= r(r+10) - 4(r+10)

= (r-4)(r+10)

r1 = 4 and r2= -10

y = e^4x and y = e^-10x

the equation will be C1e^4x + C2e^-10x