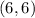Question

Hi!! Can someone answer this question please & only list the coordinates, will be listing 5 more questions ❤️

Answer 1

`M(6, 6)`

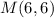
Explanation:

Given:

Endpoints of a line segment, T(6, 3) and U(6, 9)

Required:

Midpoint, M, of line segment TU

✍️Solution:

Apply the midpoint formula, which is given as:
`M((x_1 + x_2)/(2), (y_1 + y_2)/(2))`.

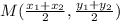Let:

`T(6, 3) = (x_1, y_1)`

`U(6, 9) = (x_2, y_2)`

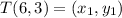
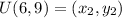
Plug in the values into the formula

`M((6 + 6)/(2), (3 + 9)/(2))`

`M((12)/(2), (12)/(2))`

`M(6, 6)`

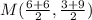
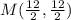
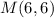
Coordinates of the midpoint, M, of line segment TU is
`(6, 6)`