Question

Jerry the mouse is running along a straight desert road at a constant velocity of 18 m/s. If a certain Tom cat wants to capture Jerry using a net dropped from an bridge that is 15m high, how much time before Jerry is under the bridge, should Tom drop the net? s How far away from the bridge is Jerry when Tom drops the net? m

Answer 1

a) t = 1.75 s

b) x = 31.5 m

Step-by-step explanation:

a) The time at which Tom should drop the net can be found using the following equation:

`y_(f) = y_(0) + v_(oy)t - (1)/(2)gt^(2)`

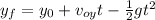
Where:

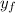`y_(f)`: is the final height = 0

y₀: is the initial height = 15 m

g: is the gravity = 9.81 m/s²

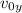`v_(0y)`: is the initial vertical velocity of the net = 0 (it is dropped from rest)

`0 = 15m - (1)/(2)9.81 m/s^(2)*t^(2)`

`t = \sqrt{(2*15 m)/(9.81 m/s^(2))} = 1.75 s`

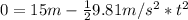
Hence, Tom should drop the net at 1.75 s before Jerry is under the bridge.

b) We can find the distance at which is Jerry when Tom drops the net as follows:

`v = (x)/(t)`

`x = v*t = 18 m/s*1.75 m = 31.5 m`

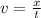
Then, Jerry is at 31.5 meters from the bridge when Jerry drops the net.

I hope it helps you!