Answer:
17190 years
Step-by-step explanation:
The exponential decay equation is:
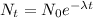
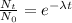
Where:
N(t) is the quantity at time t
N₀ is the initial amount
λ is the decay constant = ln(2)/t(1/2)
t(1/2) is the half-life
Since the ratio of carbon-14 to carbon-12 is 12.5%, we have that:
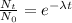
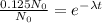
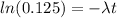
By solving the above equation for t:
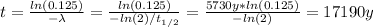
Therefore, the site is 17190 years old.
I hope it helps you!