Question

The amount Diego charges to detail an SUV is proportional to the time it takes him to detail the vehicle. Diego charges $37.50 to detail a SUV that takes 2.5 hours to complete. Which equation models the amount in dollars, d, Diego charges when it takes him h hours to detail the vehicle? Question 1 options: h = 15d d = 15h d = 93.75h h = 93.75

Answer 1

`d = 15h`

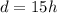
Explanation:

Given

`Charges\ \alpha\ Time`

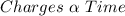
Represent charges with d and time with h

So:

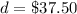`d = \$37.50` when
`t = 2.50\ hours`

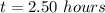
Required

Determine the formula

`Charges\ \alpha\ Time`

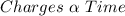
In other words,

`d\ \alpha\ h`

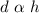
Convert to an equation

`d = k * h`

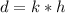
Where

k = constant of proportion

Substitute values for Charges and Time

`37.50 = k * 2.5`

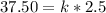
Solve for k

`k = 37.50/2.50`

`k = 15`

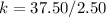
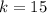
Substitute 15 for k in
`d = k * h`

`d = 15 * h`

`d = 15h`

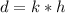
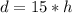
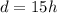
The above formula models the situation