Answer:
a) The equation giving the boiling point of the liquid is
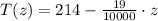 .
.
b) The boiling point of the liquid at 2400 feet is 209.44 degrees Fahrenheit.
Explanation:
a) From the statement of the problem, we understand that boiling point of a liquid is represented by the following linear function in terms of altitude:
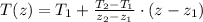 (Eq. 1)
(Eq. 1)
Where:
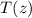 - Temperature as a function of altitude, measured in degrees Fahrenheit.
- Temperature as a function of altitude, measured in degrees Fahrenheit.
 - Altitude, measured in degrees Fahrenheit.
- Altitude, measured in degrees Fahrenheit.
 ,
,
 - Lower and higher temperatures, measured in degrees Fahrenheit.
- Lower and higher temperatures, measured in degrees Fahrenheit.
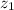 ,
,
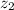 - Lower and higher altitudes, measured in feet.
- Lower and higher altitudes, measured in feet.
If we know that
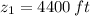 ,
,
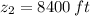 ,
,
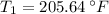 ,
,
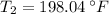 , then we find that the equation giving the boiling point of the liquid is:
, then we find that the equation giving the boiling point of the liquid is:
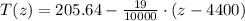
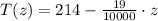 (Eq. 2)
(Eq. 2)
The equation giving the boiling point of the liquid is
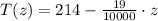 .
.
b) If we know that
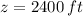 , then the boiling point of the liquid at such altitude is:
, then the boiling point of the liquid at such altitude is:

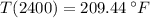
The boiling point of the liquid at 2400 feet is 209.44 degrees Fahrenheit.