Question

The table of values models the quadratic function y = x2 + 7x - 9. What are the missing y-values in the table for the x-values?

x -2. -1. 1. 0 1 2
y. _ _ _ _ _ _
A) - 19, -15,-9, -15, -19
B) -19, -15, -9, -1,9
C) 19,15,9,1,-9
D 19, 15, 9, 1,9​

Answer 1

D

Explanation:

Answer 2

For the quadratic function y = x^2 + 7x - 9, the missing y-values in the table are: -19, -15, -1, -9, -1, 9, corresponding to the x-values -2, -1, 1, 0, 1, 2. Thus, the correct option is B.

To find the missing y-values for the given quadratic function
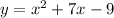`\(y = x^2 + 7x - 9\)`, you can substitute each x-value into the function and calculate the corresponding y-value.

Let's substitute each x-value into the function:

y(-2) = (-2)^2 + 7(-2) - 9 = 4 - 14 - 9 = -19

y(-1) = (-1)^2 + 7(-1) - 9 = 1 - 7 - 9 = -15

y(1) = (1)^2 + 7(1) - 9 = 1 + 7 - 9 = -1

y(0) = (0)^2 + 7(0) - 9 = 0 - 0 - 9 = -9

y(1) = (1)^2 + 7(1) - 9 = 1 + 7 - 9 = -1

y(2) = (2)^2 + 7(2) - 9 = 4 + 14 - 9 = 9

So, the complete table is:

x : -2, -1, 1, 0, 1, 2

y : -19, -15, -1, -9, -1, 9

Therefore, the correct option is:

**B) -19, -15, -9, -1, -9**